Intervals in Fault-Free Error Modeling for GNSS Applications

Nowadays, the Global Navigation Satellite System (GNSS) is widely applied for transportation navigation. These applications can be safety-critical, such as autonomous driving, where high-integrity performance of the navigation system must be ensured. Therefore, approaches to integrity monitoring (i.e., the assessment of trust that we can put into a navigation solution) have been investigated to protect users against potential integrity threats. Crucial questions include: how representative the point positions are and how their uncertainty can be safely bounded. In this regard, the effective uncertainty budget is of vital importance. This does not only mean the random variability of the observations (stochasticity), but also remaining systematic errors as a second – sometimes dominant – component.

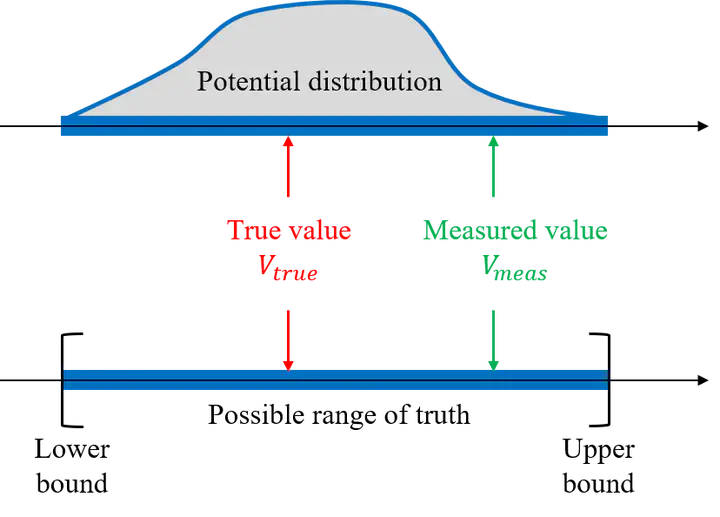
Intervals can be seen as a natural way to bound observation uncertainty in navigation systems, since they are in principle free of any assumption about probability distributions and can thus describe adequately remaining systematic effects. Transferring the uncertainty from the observation domain to the state domain, such as the position and pose, the uncertainty is represented as a set-value, e.g., polytope, zonotope and interval box. This is applicable in navigation integrity monitoring as an alternative approach for error bounding, in contrast to conventional stochastic handling. The critical issue is how to determine the observation uncertainty interval properly.

In this talk, we report methods we have applied in the context of GNSS range-based positioning and show examples of uncertainty intervals due to different error sources in GNSS signal propagation. After that, we discuss how the subsequent set representation can be used in fault-free error modeling for GNSS integrity monitoring.